Definición y tipo de rotaciones
Una Rotación es una modificación sencilla sobre la estructura de un árbol binario de búsqueda, que permite mantener la propiedad de orden.
Hay dos tipos de rotaciones básicas llamadas rotaciones simples
- Rotación Simple Derecha
- Rotación Simple Izquierda
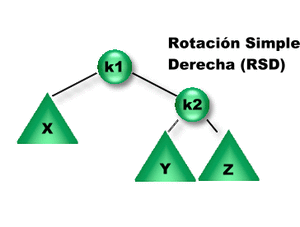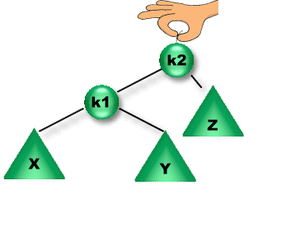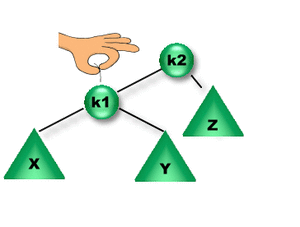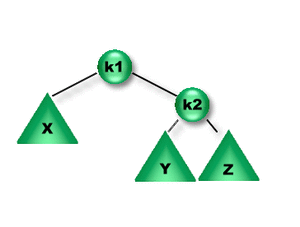
En la figura anterior podemos observar que una rotación simple derecha sobre K1 hace que K2 pase a ser la nueva raíz y una rotación simple izquierda sobre K2 hace que K1 pase a ser la nueva raíz. En ambos casos los subárboles de K1 y K2 se reacomodan respetando la propiedad de orden.
Veamos como funcionan las rotaciones sobre el siguiente árbol:
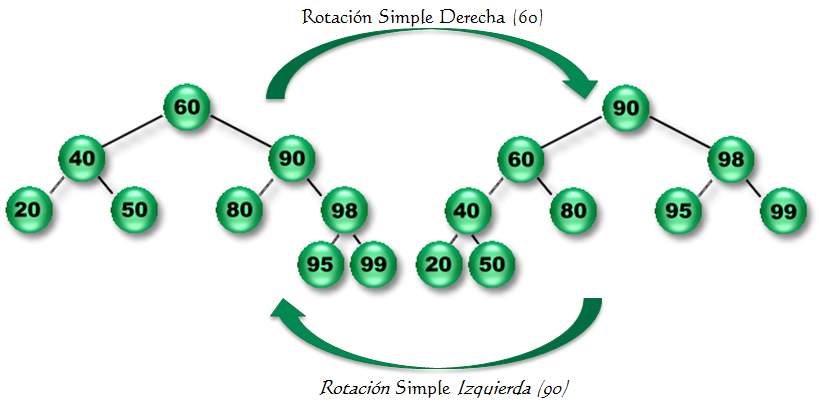
Observemos que:
-
el árbol de la derecha es el resultado de la Rotación Simple Derecha sobre el nodo 60.
-
el árbol de la izquierda es el resultado de la Rotación Simple Izquierda sobre el nodo 90.
-
la propiedad de orden que se cumplía antes de la rotación se mantuvo después de cada una de ellas.
La rotación simple derecha sobre el nodo 60 pivotea alrededor del enlace entre 60 y su hijo derecho 90, haciendo que:
- el hijo izquierdo de 90 pase a ser el hijo derecho de 60
- el 60 pase a ser el hijo izquierdo de 90.
- el 90 resulte ser la nueva raíz
La rotación simple izquierda sobre el nodo 90 pivotea alrededor del enlace entre 90 y su hijo izquierdo (60), haciendo que:
- el hijo derecho de 60 pase a ser el hijo izquierdo de 90
- el 90 pase a ser el hijo derecho de 60
- el 60 resulte ser la nueva raíz.