Consideraciones en el proceso de Inserción
La operación de inserción podría destruir la propiedad de balanceo del árbol AVL
Problema: Desbalanceo de nodos
El proceso de inserción en árboles AVL es igual al de los árboles binarios de búsqueda salvo que una vez insertado el elemento se debe tener en cuenta si esta inserción produjo un desbalanceo. Veamos que sucede en los siguientes casos:
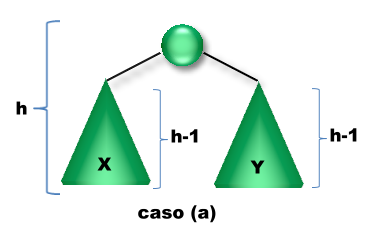
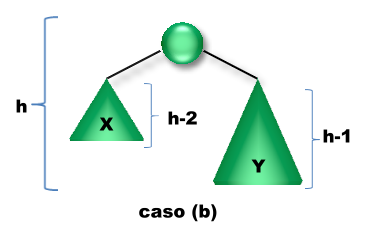
Solución: Rebalancear aplicando Rotaciones
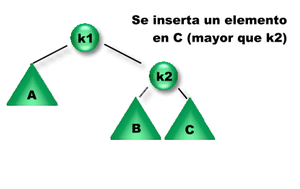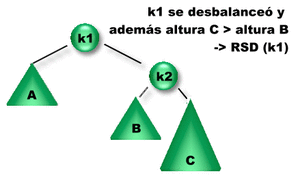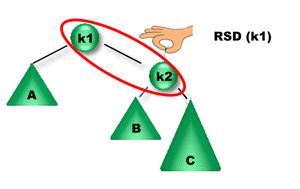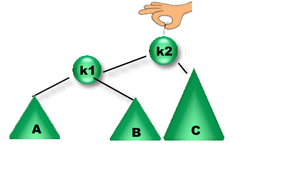
Veamos gráficamente y en detalle las situaciones posibles en el caso b:
|
Se insertó un elemento en el subárbol C. Como la diferencia entre las alturas de los subárboles derecho e izquierdo de K1 es igual a 2, K1 se desbalanceó => Es necesario rebalancearlo para reestablecer la propiedad de balanceo de K1. ¿Qué rotación se debe aplicar?
Como la altura del subárbol derecho de K2 es mayor que la altura del subárbol izquierdo de K2 se debe aplicar una Rotación Simple Derecha sobre K1 (RSD(K1)).
|
|
|
---------------------------------------------------------------------------------------------------------- |
|
|
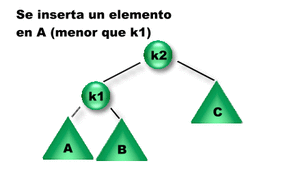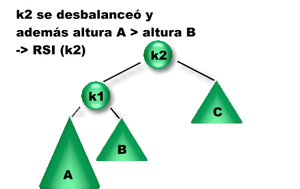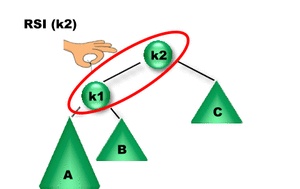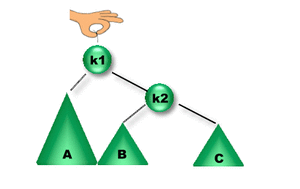
Se insertó un elemento en el subárbol A. Como la diferencia entre las alturas de los subárboles izquierdo y derecho de K2 es igual a 2, K2 se desbalanceó => Es necesario rebalancearlo para reestablecer la propiedad de balanceo de K2. ¿Qué rotación se debe aplicar? Como la altura del subárbol izquierdo de K1 es mayor que la altura del subárbol derecho de K1 entonces se debe aplicar una Rotación Simple Izquierda sobre K2 (RSI(K2)).
|
|
|
---------------------------------------------------------------------------------------------------------- |
|
|
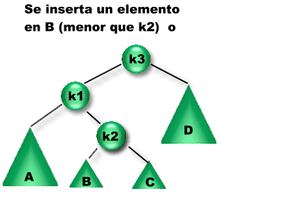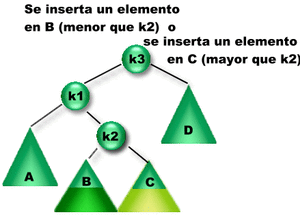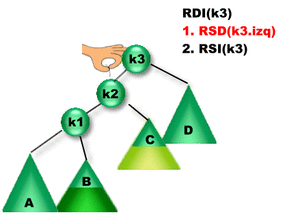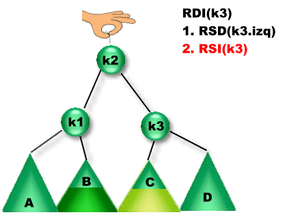
Se insertó un elemento en el subárbol B o el C. Como la diferencia entre las alturas de los subárboles derecho e izquierdo de K1 es igual a 2, K1 se desbalanceó => Es necesario rebalancearlo para reestablecer la propiedad de balanceo de K1. ¿Qué rotación se debe aplicar? Como la altura del subárbol derecho de K1 es mayor que la altura del subárbol izquierdo de K1 entonces se debe aplicar una Rotación sobre el subárbol Derecho de K1. Como la altura del subárbol izquierdo de K3 es mayor que la del derecho, entonces se aplica una Rotación Doble Derecha sobre K1 (RDD(K1)). |
|
|
---------------------------------------------------------------------------------------------------------- |
|
|
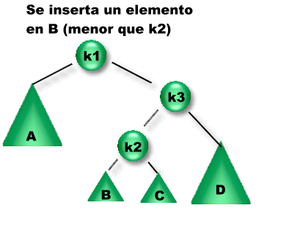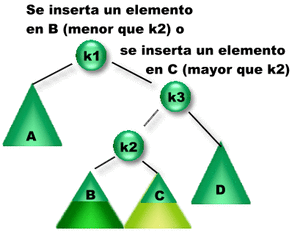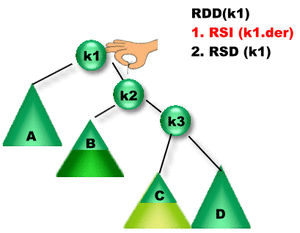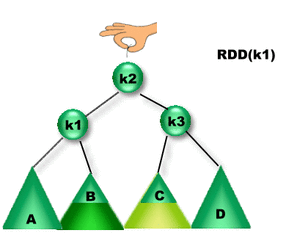
Se insertó un elemento en el subárbol B o el C. Como la diferencia entre las alturas de los subárboles izquierdo y derecho de K3 es igual a 2, K3 se desbalanceó => Es necesario rebalancearlo para reestablecer la propiedad de balanceo.
¿Qué rotación se debe aplicar? Como la altura del subárbol izquierdo de K3 es mayor que la altura del subárbol derecho de K3 entonces se debe aplicar una Rotación sobre el subárbol Izquierdo de K3. Como la altura del subárbol derecho de K1 es mayor que la del derecho, entonces se aplica una Rotación Doble Izquierda sobre K3 (RDI(K3)). |
|