Si dos cabezas piensan mejor que una, entonces ¿qué tan buenas serán varias cabezas? Para saberlo, una profesora de estadística llenó un frasco con caramelos y salió a preguntarle a la gente "¿Cuántos caramelos hay adentro del frasco?". Les dio una pista "La cantidad de caramelos la elegí al azar entre 50 y 100".
Primero le preguntó a cada uno de sus alumnos por separado. Hizo un histograma de las estimaciones que ellos ofrecieron y observó cierta uniformidad en las respuestas. Claro, con la ayuda que la profesora les ofreció eligieron al azar un número entre 50 y 100. El rango medio de las estimaciones fue de (75 ± 15) caramelos.
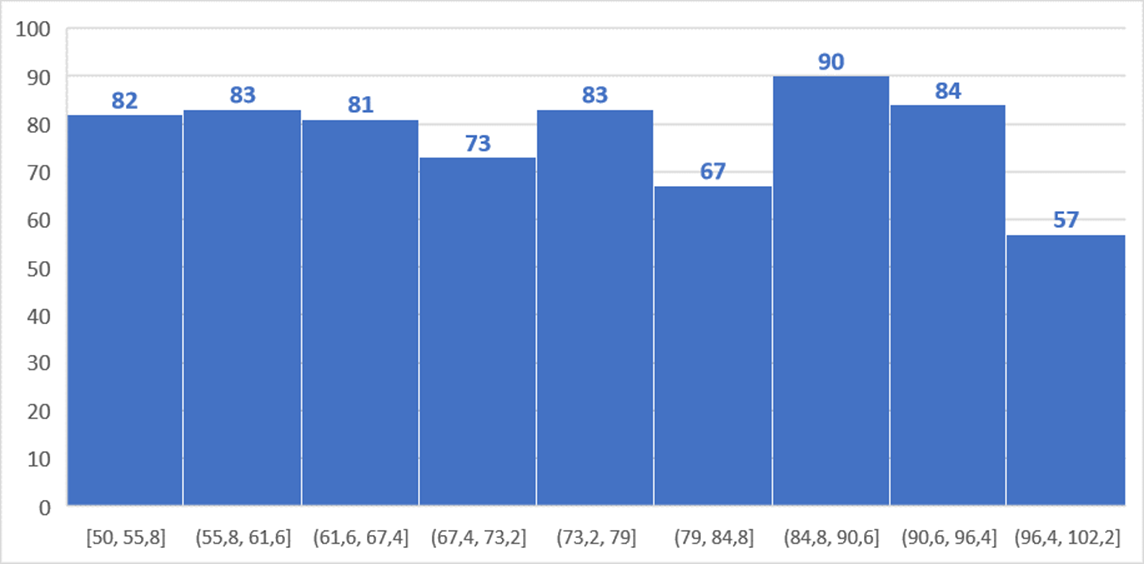
Se propuso salir diez veces al día a la calle y hacerle la pregunta a 2 personas, cada vez. Anotar sus estimaciones y calcular el promedio cada vez, redondeando al entero. Le pidió ayuda a su esposo y sus tres hijos para que hicieran lo mismo cada día. Así durante una semana. Reunió los 350 promedios de estimaciones de cada grupo de 5 personas, encontró que variaban entre 51 y 100, y calculó el rango medio. Reportó un valor medio de 75 caramelos y una variabilidad de 11 de estas golosinas. ¡Esta vez los promedios de estimaciones fueron más precisos!
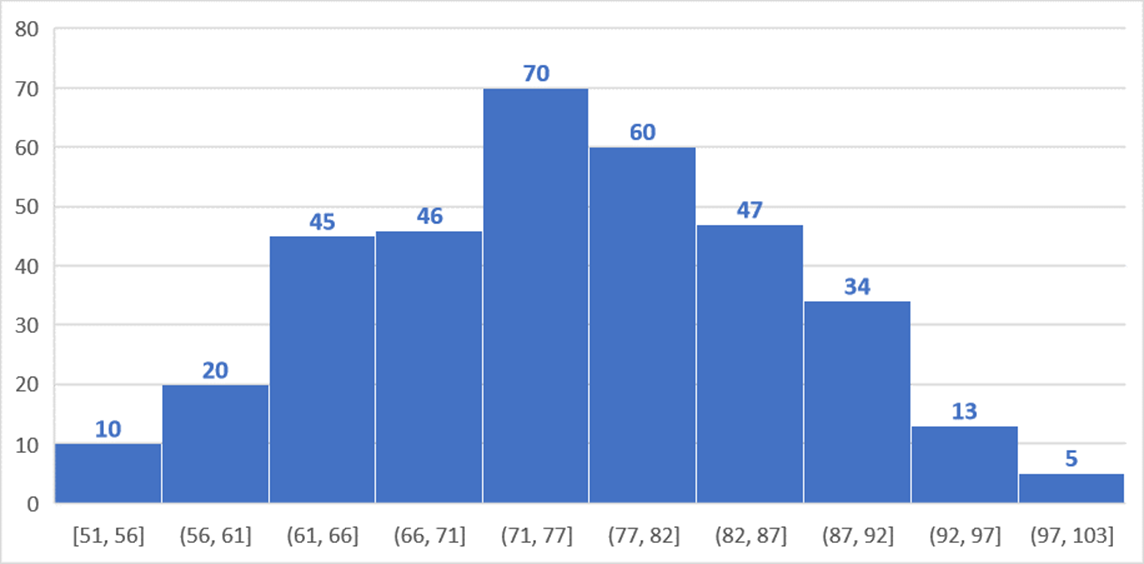
Convenció a su familia de que la siguiera ayudando en su experimento y que saliera otra semana más a encuestar a la gente. Esta vez considerando 50 personas cada vez. Encontró que los promedios se encontraban en un rango de 69 a 82 caramelos, siendo el valor medio 75, ¡pero la variabilidad de sólo 2 caramelos!
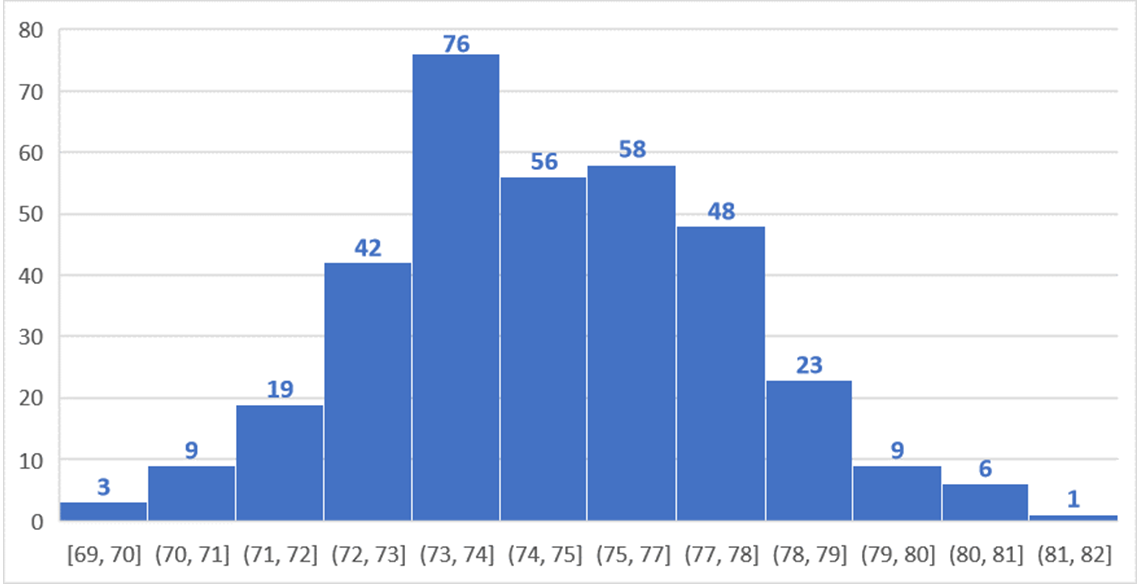
Contar con 350 muestras, en los dos casos, le permitió estar segura que las distribuciones empíricas serían buenas aproximaciones a las distribuciones muestrales correspondientes. ¿Sabés cuántos caramelos había puesto esta profesora en el frasco? ¡75!
Las distribuciones de los promedios de 2 y 50 estimaciones son...
