Laboratorio

Partes de la pantalla

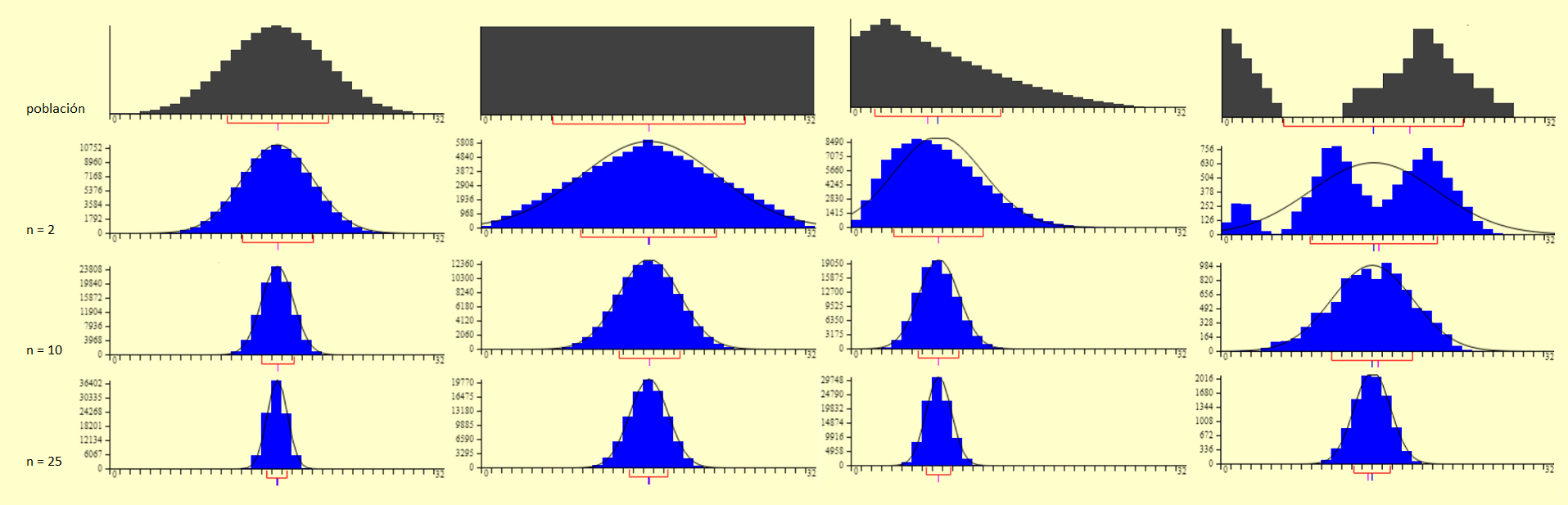
La pantalla incluye cuatro áreas de gráficos. La distribución representada en la parte superior de la pantalla es la población de la que se toman las muestras. Inicialmente se observa una distribución normal acompañada por algunos de sus parámetros, en especial la media (mean), la mediana (median) y la desviación estándar (sd). La media de la distribución está indicada por una pequeña línea azul y la mediana por una pequeña línea fucsia. Cuando la media y la mediana son iguales, las dos líneas se superponen. La línea roja se extiende una desviación estándar en cada dirección respecto de la media. Los colores utilizados en el histograma se corresponden con los empleados para mostrar los valores de estos parámetros a la izquierda del histograma.

El segundo histograma representan los datos de la muestra. Este histograma está inicialmente en blanco. Los histogramas tercero y cuarto muestran la distribución de los estadísticos calculados a partir de los datos de muestra. La cantidad de muestras (repeticiones) en las que se basan el tercer y cuarto histograma se indica con la etiqueta "Reps".

Operaciones básicas

La simulación está configurada para muestrear inicialmente cinco números de la población ("N=5" en el menú desplegable a la derecha del tercer histograma), calcular el promedio de los cinco números y graficarlo. Al hacer clic en el botón "Animated" aparecerán los cinco números en el segundo histograma. El promedio de los cinco números se calculará y se representará en el tercer histograma. Haciendo ésto varias veces se puede ver cómo se forma la distribución de esos promedios. Una vez que veas el funcionamiento con algunos casos, es posible acelerar las cosas tomando 5, 1.000 o 10.000 muestras a la vez, haciendo clic en los botones correspondientes a la derecha del segundo histograma.

Modificación de variables

La simulación permite modificar diferentes variables como el estadístico a calcular a partir de las muestras, el tamaño de estas últimas, la distribución de la población, y la posibilidad de comparar la distribución muestral con la normal.

Elección del estadístico

Si bien es posible calcular diferentes estadísticos a partir de las muestras eligiendo las diferentes opciones del menú emergente a la derecha del tercer histograma, en este material nos interesa analizar el comportamiento del promedio o media muestral (opción "Mean"). Es importante que distingas bien cuándo se trata de características de la muestra y cuándo de la población.

Selección del tamaño de muestra

El tamaño de cada muestra se puede establecer en 2, 5, 10, 16, 20 o 25 en el segundo menú emergente a la derecha del tercer gráfico. Es importante no confundir el tamaño de la muestra con el número de muestras (opciones del segundo histograma).

Comparación con la distribución normal

La opción "Fit normal" permite ver la curva de una distribución normal superpuesta sobre la distribución muestral simulada.

Cambiar la distribución de la población

Se puede cambiar la población haciendo clic en el menú emergente a la derecha del histograma superior. Se ofrecen algunas opciones por defecto (normal, uniforme, asimétrica), y es posible configurar cualquier otra distribución mediante la opción "Custom" y haciendo clic con el mouse sobre el área del primer histograma y arrastrando.  

Distribución muestral

Si necesitás repasar el concepto de distribución muestral de la media, empezá por acá. El concepto puede experimentarse y generalizarse para otros estadísticos:

1. Elegí una distribución para la población (por ejemplo, la normal) y la media (mean) como estadístico.
2. Hacé clic en el botón "Muestra animada". Se tomarán muestras de cinco valores de una distribución normal (mirá los valores de los parámetros de la izquierda para saber cuál es) y se representarán en el segundo histograma. La media de la muestra, es decir el promedio, se calculará y representará en el tercer histograma. Repetí el procedimiento unas tres o cuatro veces o hasta que comprendas cómo se crea la distribución de promedio.
3. Hacé clic en el botón "5" para simular cinco muestras de cinco valores cada una. Los cinco promedios serán graficados. Hacé clic en "10.000" o "100.000" hasta que la distribución de los promedios se haya estabilizado. 

La distribución que se obtiene a medida que el número de muestras aumenta es la distribución muestral de la media o promedio de cinco valores de una normal (si elegiste esa distribución para la población). Con 10.000 muestras obtenés una excelente aproximación. Podés aproximar la distribución muestral de la media para otros tamaños de muestra y para otras distribuciones poblacionales. ¿Te animás?

Teorema Central del Límite

Si recordás qué significa la distribución muestral de la media o promedio, seguí los pasos que se indican a continuación para experimentar diferentes situaciones que te permitan comprender las condiciones e implicancias del TCL.

1. Elegí la distribución uniforme (uniform) para la población, el promedio (mean) como estadístico, y el tamaño de las muestras (podés comenzar por "N=2") y obtené la distribución muestral de la media (acordate que con unas 10.000 muestras se tiene una excelente aproximación). Observá y analizá los resultados obtenidos.
2. Repetí el procedimiento del paso 1 para diferentes tamaños muestrales ("N=5" a "N=25"). Observá y analizá los resultados obtenidos.
3. Repetí los pasos 1 y 2 para una distribución sesgada (skewed) y una personalizada (custom). Observá y analizá los resultados obtenidos.

Prestá atención a las siguientes cuestiones:

• • • • ¿Qué sucede a medida que el tamaño muestral aumenta?
• • • • ¿Qué distribución te parece que tiene la media muestral o promedio?
      • ¿Cuál es la media del promedio y qué relación guarda con la media poblacional?
      • ¿Cuál es la varianza de la media muestral y qué relación guarda con la varianza poblacional?