 El conocido personaje, dueño del pub que te presentamos en la sección Diagnóstico, pudo recolectar algunos datos para investigar cambios que mejoren la calidad del servicio. En primer lugar, quiere tratar de resolver dos problemas que entiende como urgentes:
El conocido personaje, dueño del pub que te presentamos en la sección Diagnóstico, pudo recolectar algunos datos para investigar cambios que mejoren la calidad del servicio. En primer lugar, quiere tratar de resolver dos problemas que entiende como urgentes:
- Las quejas de sus clientes por los porrones que no llegan a la mesa tan llenos como debieran.
- La solicitud de dos de sus tres bartender para llegar una hora más tarde por cuestiones familiares. Sabe que una sola persona puede atender cómodamente a un par de clientes por minuto, pero una mayor cantidad reduciría notablemente la calidad del servicio.
 Las quejas de los clientes
Las quejas de los clientes
Como vimos en la sección Diagnóstico, cada vez que se quiere llenar un porrón, las canillas expenden una cierta cantidad de cerveza que, medida en mililitros, puede ajustarse a una distribución acampanada de media 365 y desvío 20. Pero no estamos seguros si esa distribución es normal, aunque tenga forma de campana. El dueño pudo recolectar datos de 30 clientes que eligió al azar un día y los resultados promedio que obtuvo no estuvieron muy lejos de las especificaciones de las canillas, porque aproximadamente fueron de (367 ± 21) mililitros.
El estadístico que va a ayudarle con su estudio le preguntó cómo había recolectado esos datos y si creía que eran representativos de todos sus clientes. El dueño está seguro que no. Los eligió todos en un mismo momento de un mismo día y quizás, en ese día y horario particular, las cosas funcionaron "bien" por alguna razón que él desconoce. El estadístico le propone entonces que elija una misma cantidad de clientes, al azar, durante "muchos" momentos. Y que, para cada uno de esos grupos calcule la cantidad promedio de cerveza que tiene cada porrón.
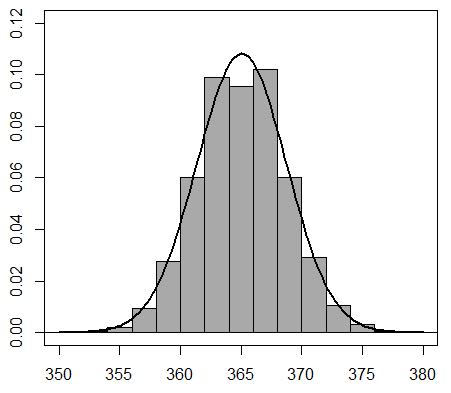
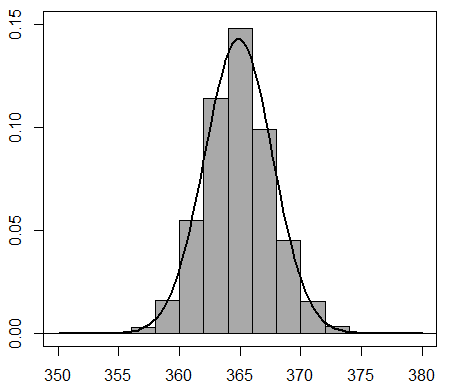
Siguiendo los consejos del estadístico, el dueño elige al azar 30 clientes en varios momentos durante "muchos" días. Calcula los volúmenes medios y hace un gráfico. Redobla la apuesta y repite el experimento pero ahora con 50 clientes. En ambos casos observa que las distribuciones muestrales de los promedios se ajustan a una curva acampanada. El Teorema Central del Límite permite afirmar que tales distribuciones son normales, ambas de media 365 mililitros. Sin embargo, las varianzas son distintas. En el caso de los promedios de 30 clientes, la varianza es 400/30. Mientras que, para 50 clientes es de 400/50. ¡Entonces parace no haber ningún problema con las cantidades de cerveza en los porrones! ¡Se sirve tanto como indican las especificaciones de las canillas!
|
Histograma de los promedios de 30 clientes |
Histograma de los promedios de 50 clientes |
Si hubiese tomado muestras aún más grandes, digamos 100, el Teorema Central del Límite le hubiera permitido afirmar que la distribución de los promedios resulta normal de media 365 y varianza 4. ¡Cada vez más concentrada, igual que en el caso de los pesos de los conejos y las extensiones de las alas de los dragones!
 Permisos para llegar más tarde
Permisos para llegar más tarde
El dueño del bar, pensando en los experimentos que hizo bajo la asistencia del estadístico piensa que, si considera varios minutos dentro de la primera hora de atención en el bar en días diferentes podrá tener una buena idea de si la cantidad promedio de clientes que ingresa es mayor a 10 o no. Y, en consecuencia, si puede o no darle permiso a sus empleados para llegar más tarde. Lo consulta con el estadístico quien lo felicita por su razonamiento.
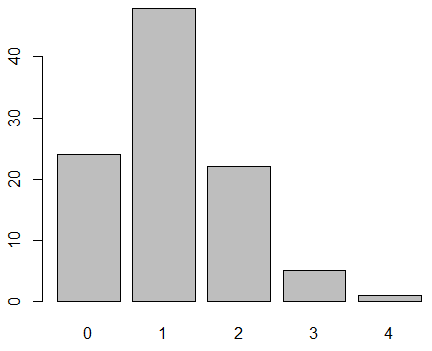 Empieza por registrar a lo largo de 1 minuto cualquiera dentro de la primer hora de trabajo de "muchos" días cuántos clientes ingresaban. Esto le permitió tener una idea de la cantidad de clientes que ingresan a su local por minuto. Como sospechaba, la mayoría de las veces ingresan uno o ninguno, ¡pero otras tantas veces ingresan dos o más!
Empieza por registrar a lo largo de 1 minuto cualquiera dentro de la primer hora de trabajo de "muchos" días cuántos clientes ingresaban. Esto le permitió tener una idea de la cantidad de clientes que ingresan a su local por minuto. Como sospechaba, la mayoría de las veces ingresan uno o ninguno, ¡pero otras tantas veces ingresan dos o más!
Pero, ya ha aprendido que es mejor trabajar con varios grupos, calcular la cantidad de clientes promedio para cada uno de esos grupos, y considerar la distribución de esos promedios. Así que echa manos al asunto. Después de algunos días, desalentado, el dueño le muestra los resultados al estadístico. "No pasó lo mismo que antes, las cantidades promedio de clientes que entran por minuto son muy dispersas, y no tienen una forma acampanada", le dijo. ¿Qué falló esta vez? ¿Que la distribución poblacional no era simétrica como en el caso de la cerveza? De ninguna manera. Conversando con el estadístico se da cuenta que ¡consideró muestras de 5 periodos de 1 minuto! ¡Era necesario que el tamaño muestral fuera al menos 30! Sobre todo en este caso, donde la distribución de la variable aleatoria original no era simétrica. Así que repite el experimento, pero ahora considerando 45 periodos de 1 minuto cada vez. ¡Ahora sí! Observa que la distribución de los promedios de clientes que entran por minuto cuando considera 45 periodos cada vez es aproximadamente normal con media un cliente y desvío estándar de 0.15 clientes.
|
|
|
¡Genial! Puede autorizar que sus bartender lleguen una hora tarde.
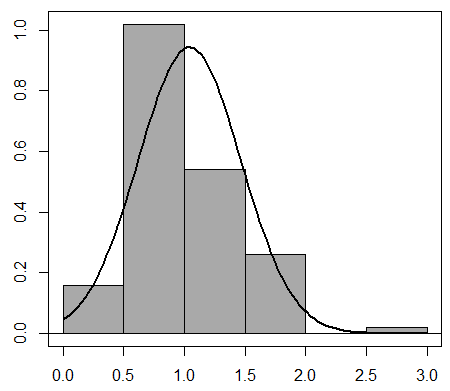 Histograma de clientes promedio por minuto en 5 periodos
Histograma de clientes promedio por minuto en 5 periodos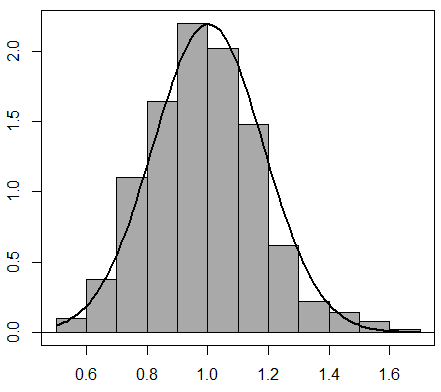 Histograma de clientes promedio por minuto en 45 periodos
Histograma de clientes promedio por minuto en 45 periodos